princip najmanjega djelovanja, integralni oblik načela klasične mehanike koji je temelj, uz D’Alembertovo načelo, za izvod Hamiltonovih (→ hamiltonijanski sustavi) i Lagrangeovih jednadžbi gibanja (→ lagrange, joseph louis de). Gibanje sustava od N materijalnih točaka može se prikazati Lagrangeovom funkcijom L (qk, q̇k, t), u kojoj su qk generalizirane koordinate, q̇k njihove derivacije po vremenu, a t vrijeme. Po principu najmanjega djelovanja za ponašanje sustava u intervalu Δt = t2 – t1 vrijedi:
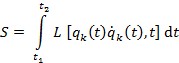 .
.
Veličina S ima općenito dimenziju nekoga djelovanja (ovisno o tome na što se Lagrangeova funkcija primjenjuje), a iz matematičkoga oblika (integrala) slijedi da putanja materijalne točke između t1 i t2 može biti minimalna ili maksimalna, odn. zbog besmislenosti rješenja po kojemu je putanja beskonačna, putanje mora biti minimalna. Veličina S naziva se i integral djelovanja ili funkcional djelovanja. Na temelju njega moguće je riješiti niz problema gibanja, npr. zakone refleksije i loma svjetlosti uz uvjet da je Δt = min između dviju točaka na putanji svjetlosne zrake. Taj je princip u integralnom obliku izrazio William Rowan Hamilton.