limes

limes (lat.: put, staza između dvaju polja; granica) (granična vrijednost), rezultat graničnoga procesa.

Limes niza je broj A kojemu se članovi niza brojeva {a_n}, n = 1, 2, …, neograničeno približuju kada broj članova niza n raste. Niz teži (konvergira) k limesu A, 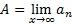odnosno a_n → A, ako razlika između limesa i n-tog člana niza |A – a_n| za veliki redni broj člana niza (n → ∞) postaje za po volji mala. Preciznije, A je granična vrijednost niza brojeva {a_n}, 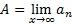, ako za svaki odabrani maleni pozitivni broj ε u zadanom nizu postoji takav broj a_n0 da je za sve članove niza koji su u nizu iza a_n0, tj. za n > n₀, njihova razlika od limesa A apsolutno manja od odabranog malenog pozitivnog broja ε. Pri grafičkom predočivanju niza na brojevnom pravcu, svaka okolina od limesa A sadrži sve članove niza osim eventualno konačno mnogo njih.

Dogovorno se uzima da je limes niza brojeva pozitivna ili negativna beskonačnost tj. lim a_n = + ∞ odnosno – ∞, ako za svaki po volji velik pozitivan broj K postoji takav član niza a_n0 da su svi članovi koji se nalaze iza njega po apsolutnoj vrijednosti veći od odabranog broja K tj. a_n > K odnosno a_n < – K za sve članove niza a_n takve da je n > n₀. Niz može imati najviše jedan limes. Ako je lim a_n = A i lim b_n = B, za postizanje granične vrijednosti vrijede ova pravila: lim (a_n ± b_n) = A ± B, lim a_nb_n = AB, lim a_n/b_n = A/B.

Limes funkcije je broj A prema kojemu se približava vrijednost funkcije f(x) kada se nezavisna varijabla x približava točki a, odnosno 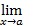f(x) = A. Funkcija f(x) ima limes jednak broju A kada joj argument x teži k točki a i ako za svaki broj ε > 0 postoji broj δ > 0 tako da vrijedi |f(x) – A| < ε za sve x za koje je |x – a| < δ. Najpoznatiji su granični procesi: tangenta u točki A krivulje kao granični položaj sekante AB kada se točka B po krivulji približava točki A; opseg (ploština) kruga kao granična vrijednost opsega (ploština) tom krugu upisanih, odnosno opisanih pravilnih višekuta kojima broj stranica neograničeno raste, itd.

Osnovni teoremi o limesima funkcija:

(1) limes konstante jednak je toj konstanti:

lim A = A;

(2) limes zbroja (razlike) konačnog broja funkcija jednak je zbroju (razlici) limesa tih funkcija:

;

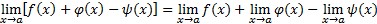(3) limes umnoška konačnog broja funkcija jednak je umnošku limesa tih funkcija:

;

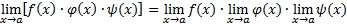(4) limes količnika dviju funkcija jednak je količniku limesa tih funkcija, ako je djelitelj različit od nule:

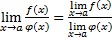, ako je .

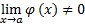Najpoznatiji limesi:

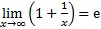, gdje je e Eulerov broj;

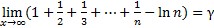, gdje je γ = 0,5772… Eulerova konstanta;

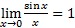, gdje je x duljina luka ili kut izražen u radijanima.