redovi, beskonačni izrazi oblika a1 + a2 + … + an + … = 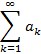 . Zbrojnici ak su članovi reda; mogu biti brojevi, vektori, matrice, funkcije i dr. pa se govori o redu brojeva, redu vektora, redu matrica, redu funkcija itd. Osnovni je slučaj da su članovi reda brojevi. Svakom redu jednoznačno je pridružen niz
. Zbrojnici ak su članovi reda; mogu biti brojevi, vektori, matrice, funkcije i dr. pa se govori o redu brojeva, redu vektora, redu matrica, redu funkcija itd. Osnovni je slučaj da su članovi reda brojevi. Svakom redu jednoznačno je pridružen niz 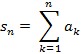 , zvan niz parcijalnih zbrojeva toga reda. Ako niz sn konvergira, tj. ako je lim sn = S, za n → ∞, konačan broj, kaže se da je red konvergentan i da je njegova zbroj S, odnosno da je divergentan ako taj limes ne postoji ili je beskonačan. Na taj se način pitanje konvergencije reda svodi na pitanje konvergencije niza. Npr. geometrijski red
, zvan niz parcijalnih zbrojeva toga reda. Ako niz sn konvergira, tj. ako je lim sn = S, za n → ∞, konačan broj, kaže se da je red konvergentan i da je njegova zbroj S, odnosno da je divergentan ako taj limes ne postoji ili je beskonačan. Na taj se način pitanje konvergencije reda svodi na pitanje konvergencije niza. Npr. geometrijski red 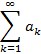 , ak = a1qk–1, kojemu članovi čine geometrijski niz, konvergentan je za | q | < 1, a zbroj mu je S = a1/1 − q, dok je divergentan za | q | ≥ 1. Divergentan je npr. i harmonijski red
, ak = a1qk–1, kojemu članovi čine geometrijski niz, konvergentan je za | q | < 1, a zbroj mu je S = a1/1 − q, dok je divergentan za | q | ≥ 1. Divergentan je npr. i harmonijski red 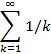 . Uvjeti i kriteriji konvergencije te izračunavanje zbroja reda osnovni su problemi teorije redova. Opći je princip konvergencije reda: da bi red konvergirao, nužno je i dovoljno da za svaki ε > 0 postoji takav prirodni broj N da za sve n > N vrijedi
. Uvjeti i kriteriji konvergencije te izračunavanje zbroja reda osnovni su problemi teorije redova. Opći je princip konvergencije reda: da bi red konvergirao, nužno je i dovoljno da za svaki ε > 0 postoji takav prirodni broj N da za sve n > N vrijedi 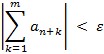 < ε kakav god bio m, ili slobodnije rečeno: zbroj ma koliko uzastopnih članova reda uzetih iza dovoljno dalekoga člana mora biti po volji malen. Važan je kriterij za utvrđivanje konvergencije reda njegova usporedba s nekim drugim konvergentnim redovima, što se zasniva na teoremu: ako je red
< ε kakav god bio m, ili slobodnije rečeno: zbroj ma koliko uzastopnih članova reda uzetih iza dovoljno dalekoga člana mora biti po volji malen. Važan je kriterij za utvrđivanje konvergencije reda njegova usporedba s nekim drugim konvergentnim redovima, što se zasniva na teoremu: ako je red 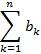 konvergentan, a za članove reda
konvergentan, a za članove reda 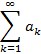 vrijedi |an| < bn za sve n veće od nekog N, tada i red
vrijedi |an| < bn za sve n veće od nekog N, tada i red 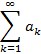 konvergira. Od posebnih kriterija konvergencije reda najvažniji su Cauchyjev i d’Alembertov: ako za red
konvergira. Od posebnih kriterija konvergencije reda najvažniji su Cauchyjev i d’Alembertov: ako za red 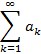 s pozitivnim članovima počevši od nekog n uvijek vrijedi an + 1/an ≤ q za neko q < 1, odnosno n√ an < q < 1, gdje je q neki konstantni broj isti za sve n, on konvergira. Ti kriteriji daju samo dovoljne uvjete konvergencije. Za neki red kaže se da konvergira apsolutno ako je red apsolutnih vrijednosti njegovih članova konvergentan, a tada je i on sam konvergentan. Za takav tip konvergencije primjenljivi su prednji kriteriji. Za apsolutno konvergentne redove vrijedi svojstvo komutativnosti članova (tj. poredaju li mu se članovi bilo kako, takav će red ostati konvergentan i zbroj se neće promijeniti), što inače ne mora biti. Npr. red s alternirajućim predznacima članova 1 – 1/2 + 1/3 – 1/4 + … konvergira i zbroj mu je ln 2. Nakon promjene redoslijeda 1 – 1/2 – 1/4 + 1/3 – 1/6 – 1/8 + … također konvergira, ali mu je zbroj 1/2 ln 2.
s pozitivnim članovima počevši od nekog n uvijek vrijedi an + 1/an ≤ q za neko q < 1, odnosno n√ an < q < 1, gdje je q neki konstantni broj isti za sve n, on konvergira. Ti kriteriji daju samo dovoljne uvjete konvergencije. Za neki red kaže se da konvergira apsolutno ako je red apsolutnih vrijednosti njegovih članova konvergentan, a tada je i on sam konvergentan. Za takav tip konvergencije primjenljivi su prednji kriteriji. Za apsolutno konvergentne redove vrijedi svojstvo komutativnosti članova (tj. poredaju li mu se članovi bilo kako, takav će red ostati konvergentan i zbroj se neće promijeniti), što inače ne mora biti. Npr. red s alternirajućim predznacima članova 1 – 1/2 + 1/3 – 1/4 + … konvergira i zbroj mu je ln 2. Nakon promjene redoslijeda 1 – 1/2 – 1/4 + 1/3 – 1/6 – 1/8 + … također konvergira, ali mu je zbroj 1/2 ln 2.
Važana su vrsta redova redovi funkcija općeg oblika 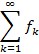 , gdje je fk niz danih funkcija definiranih na istom skupu i s vrijednostima u skupu realnih brojeva. Ako za svako x red
, gdje je fk niz danih funkcija definiranih na istom skupu i s vrijednostima u skupu realnih brojeva. Ako za svako x red 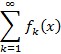 konvergira i označi li se zbroj s f(x), f je funkcija definirana na istom skupu kao fk. Tada se kaže da red funkcija
konvergira i označi li se zbroj s f(x), f je funkcija definirana na istom skupu kao fk. Tada se kaže da red funkcija 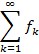 konvergira i da mu je zbroj funkcija f. Među redovima funkcija posebno su važni redovi potencija općeg oblika
konvergira i da mu je zbroj funkcija f. Među redovima funkcija posebno su važni redovi potencija općeg oblika 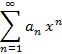 , jer se s pomoću njih mogu prikazati mnoge funkcije (→ maclaurin, colin; taylor, brook), kao npr. sin x = x – x³/3! + x5/5! – …, ex = 1 + x + x²/2! + x³/3! + …
, jer se s pomoću njih mogu prikazati mnoge funkcije (→ maclaurin, colin; taylor, brook), kao npr. sin x = x – x³/3! + x5/5! – …, ex = 1 + x + x²/2! + x³/3! + …
U matematičkoj analizi značajni su i trigonometrijski redovi, poznati kao Fourierovi redovi, kojima se može prikazati periodična funkcija f(x) s periodom T (koja ispunjava još neke uvjete) u obliku:  , gdje su koeficijenti dani s
, gdje su koeficijenti dani s 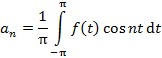 ,
, 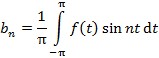 , T = 2π. (→ fourierova transformacija; fourierov integral)
, T = 2π. (→ fourierova transformacija; fourierov integral)