Taylor [tẹi'lə], Brook, engleski matematičar (Edmonton, 18. III. 1685 – London, 29. XII. 1731). Diplomirao na Sveučilištu u Cambridgeu (1709). Od 1712. bio je član Royal Society, a 1714–18. njegov tajnik. Po njem je nazvan krater na Mjesecu (Taylor). Pridonio razvoju infinitezimalnoga računa i mehanike. U djelu Izravna i inverzna metoda razvoja (Methodus incrementorum directa et inversa, 1715) objavio je svoj najvažniji rezultat: prikazivanje funkcija u obliku polinoma, odn. reda, danas poznato kao Taylorova formula, odn. Taylorov red. U djelu Linearna perspektiva (Linear Perspective, 1715) matematički je istraživao projekcije ravnih linija koje nisu paralelne s ravninom slike. Bavio se i problemom titranja žice, termometrima, zakonitostima magnetske privlačnosti i dr.
Taylorova formula omogućuje aproksimaciju neke funkcije polinomom. Ako funkcija f ima u točki a neprekidne derivacije do uključivo n-te, tada za sve x iz nekoga intervala oko a vrijedi:
ƒ(x) = ƒ(a) + ƒ'(a)(x − a) + ƒ''(a)/2! (x − a)² + … + ƒ(n)(a)/n! (x − a)n + Rn (x),
gdje je Rn (x) tzv. ostatak, tj. pogreška koja se čini ako se funkcija f(x) zamijeni Taylorovim polinomom n-toga stupnja. Ako f ima u okolini od a neprekidne derivacije do reda n + 1, onda za svako x iz te okoline postoji b iz segmenta [a, x], tako da je:
R(n) (x) = ƒ(n−1)(b)/(n−1)! (x − a)n+1 (tzv. Lagrangeov ostatak).
Taylorov red red potencija, koji uz određene uvjete predočuje danu funkciju. Ako funkcija f ima sve derivacije u okolini točke a i ako za ostatak Rn u Taylorovoj formuli vrijedi lim Rn (x) = 0 za sve x iz te okoline, tada vrijedi: 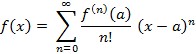 , pa se kaže da je funkcija f(x) razvijena u Taylorov red u okolini točke a. Ako je a = 0, Taylorov red naziva se Maclaurinov red.
, pa se kaže da je funkcija f(x) razvijena u Taylorov red u okolini točke a. Ako je a = 0, Taylorov red naziva se Maclaurinov red.