Lorentzove transformacije [lo:'rəncove ~] (po Hendriku Antoonu Lorentzu), algebarske linearne relacije koje povezuju prostorne i vremenske koordinate (x, y, z, t) nekoga fizičkog događaja u mirnome koordinatnom sustavu S (x, y, z, t) s pripadajućim koordinatama (x', y', z', t') u koordinatnom sustavu S' (x', y', z', t') koji se prema sustavu S giba uzduž osi x stalnom brzinom v. Izvode se, dokazuju i tumače iz dva postulata Einsteinove specijalne teorije relativnosti (1905): 1. postulata o konstantnosti brzine svjetlosti c u svim inercijskim sustavima bez obzira na brzinu gibanja sustava, izvora ili detektora svjetlosti, te 2. postulata o kovarijantnosti prirodnih zakona koji moraju imati isti oblik u svim inercijskim sustavima. Polazeći od toga da se svjetlosni signali (fotoni) šire brzinom c u oba sustava i da se pravocrtna gibanja iz jednoga, vide i u drugom sustavu i obratno (x = ct i x' = ct'), kao i od načela relativnosti (zamjene uloge sustava S i S' i koordinata u njima), dobivaju se uz odgovarajući algebarski formalizam Lorentzove transformacije u obliku:
x' = x − vt/√ 1 − β² , y' = y, z' = z,
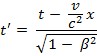 ,
,
gdje je β = v/c, a γ = 1/√ 1 − β² uobičajeno se naziva Lorentzovim faktorom. Obratne (inverzne) transformacije dobivaju se zamjenom v s –v u već napisanim relacijama (npr. x = x' + vt'/√ 1 − β² , y = y", … itd.). Posljedice su Lorentzovih transformacija u sustavu koji se giba brzinom bliskom brzini svjetlosti u odnosu na promatrača u sustavu koji miruje relativistička dilatacija vremena (vrijeme teče sporije) i relativistička kontrakcija dužine (skraćivanje tijela) u smjeru gibanja.
Jedna je od temeljnih simetrija u fizici invarijantnost fizikalnih zakona na Lorentzove transformacije (relativistička invarijantnost): jednadžbe fizike u svakom teoretskom pokušaju trebaju imati isti oblik u svim inercijskim sustavima. U modernoj fizici elementarnih čestica, invarijantnost se općenito postiže zapisom veličina i jednadžbi u četverovektorskoj formulaciji, po uzoru na četiri koordinate prostor-vremena u specijalnoj teoriji relativnosti.