matrica (lat. matrix, genitiv matricis: matica).
1. U matematici, pravokutna tablica matričnih elemenata, brojeva ili matematičkih objekata, koja sažeto prikazuje informacije o matematičkim sustavima:
 .
.
Horizontalni niz elemenata u matričnoj tablici naziva se redak, a uspravni stupac. Matrica je tipa (n, m) kad ima n redaka i m stupaca.
Vrste matrica
Redna matrica sadrži samo jedan redak (1, m), a stupčana matrica sadrži samo jedan stupac (n, 1). Na primjer: [1 2 3], 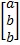 .
.
Kvadratna matrica je matrica kojoj je broj redaka jednak broju stupaca, tj. n = m. Trag matrice je zbroj elemenata na glavnoj dijagonali kvadratne matrice, a determinanta je broj pridružen kvadratnoj matrici.
Dijagonalna matrica je kvadratna matrica kojoj su svi elementi izvan glavne dijagonale jednaki nuli, tj. anm = 0 kad je n ≠ m, na primjer:
 .
.
Gornja trokutasta matrica je kvadratna matrica kojoj su svi elementi ispod dijagonale jednaki nuli, tj. anm = 0 kad je n > m, na primjer:
 .
.
Donja trokutasta matrica je kvadratna matrica kojoj su svi elementi iznad dijagonale jednaki nuli, tj. anm = 0 kad je n < m, na primjer:
 .
.
Jedinična matrica I kvadratna je matrica takva da je pomnožena s bilo kojom matricom odgovarajućega reda jednaka toj matrici, tj. IA = A, te također AI = A, a njezini su elementi amm = 1 za svaki m te anm = 0 za m ≠ n na primjer:
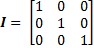 .
.
Inverzna matrica neke matrice A je matrica sa svojstvom AA–1 = A–1A = I. Matrice mogu imati samo jednu inverznu matricu, a neke matrice nemaju ni jednu.
Regularna matrica je kvadratna matrica koja ima inverznu matricu, a singularna matrica je kvadratna matrica koja nema inverznu matricu.
Osnovne operacije
Zbrajanje matrica moguće je samo ako matrice imaju jednak broj redaka i stupaca, a zbrajaju se elementi matrice koji se nalaze na istim položajima u tablici. Ako je A matrica tipa (n, m) s elementima anm, i ako je B matrica tipa (n, m) s elementima bnm, zbroj matrica A i B jest matrica C = A + B s elementima cnm = anm + bnm.
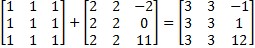 .
.
Množenje matrice brojem izvodi se tako da se svaki element matrice pomnoži brojem. Ako je α broj, umnožak broja α i matrice A je matrica D = α A s elementima dnm = α anm. Na primjer:
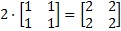 .
.
Množenje matrica moguće je samo ako matrica ima broj redaka jednak broju stupaca matrice kojom množi. Ako je A matrica tipa (n, m) i ako je B matrica tipa (m, p), njihov produkt C = AB matrica je tipa (n, p) s elementima cnm = Σ ank bkm = an1 b1m + an2 b2m + … + ant btm. Na primjer:
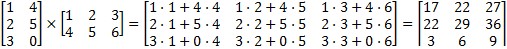 .
.
Množenje matrica nije komutativno, AB ≠ BA. Dijeljenje matrica svodi se na množenje inverznom matricom.
Transponiranje matrice postiže se zamjenom njezinih redaka i stupaca. Ako je A matrica tipa (n, m) s elementima aij, njezina transponirana matrica A⊤ ima elemente (A⊤)nm = amn, što se kod kvadratne matrice može interpretirati i kao zrcaljenje s obzirom na dijagonalu. Kvadratna matrica je simetrična ako vrijedi A = A⊤, tj. anm = amn za sve n, m, a antisimetrična ako vrijedi A⊤ = −A, tj. anm = −amn za sve n, m. Na primjer:
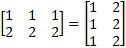 .
.
Primjena
Matrice su se sredinom XIX. st. počele primjenjivati za pojednostavljeno rješavanje sustava linearnih jednadžbi, danas se široko primjenjuju u klasičnoj mehanici, elektromagnetizmu, kvantnoj mehanici, teoriji vjerojatnosti, statistici, ekonomiji, elektrotehnici, kompjuterskom programiranju i dr. (→ vektorski prostor)
2. U strojarstvu, naziv za alat ili dio alata za deformacijsko oblikovanje metala postupcima istiskivanja (isprešavanja) šipaka, cijevi i profila, dubokog vučenja limenih proizvoda te provlačenja žice, šipkastih profila i cijevi. Matricom se naziva i alat oštrih ravnih bridova kojim se izrađuju predmeti od lima prosijecanjem, štancanjem ili finim štancanjem, a upotrebljava se u paru s patricom (žigom). (→ duboko vučenje; prosijecanje; provlačenje)
3. U tiskarstvu, mjedeni ili brončani kalup s utisnutim slovnim znakom, kakav se nekoć u slagarskim strojevima slagao u retke i potom služio za odlijevanje olovnoga sloga. (→ tiskarski slog)