račun varijacija (varijacijski račun), grana matematičke analize koja se bavi problemom egzistencije, jedinstvenosti i određivanja funkcija koje zadanomu funkcionalu daju ekstremnu vrijednost. Funkcional je realna funkcija koja ovisi o jednoj funkciji ili više funkcija zadanih svojstava kao neovisnih varijabli. Velik broj stvarnih problema može se svesti na minimizaciju ili maksimizaciju funkcionala oblika
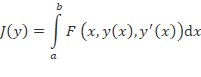 ,
,
uz odgovarajući odabir funkcije F i skupa funkcija C (y ∈ C).
Problematika računa varijacija srodna je problematici određivanja ekstrema funkcije, s tom razlikom što je pri određivanju ekstrema riječ o određivanju vrijednosti argumenta za koji funkcija poprima ekstrem, dok se u računu varijacija traže funkcije određenih svojstava koje promatranomu funkcionalu daju ekstremnu vrijednost.
Povijesni razvoj
Prvi ozbiljan varijacijski problem i način njegova rješavanja opisao je Isaac Newton u djelu Matematički principi filozofije prirode (1687). Istraživao je za koji će oblik tijela, pri gibanju kroz fluid stalnom brzinom, otpor fluida biti najmanji.
Jakob Bernoulli postavio je (1696) tzv. problem brahistokrone, krivulje koja u vertikalnoj ravnini spaja dane dvije točke različitih visina, po kojoj bi se moralo gibati tijelo pod utjecajem gravitacije, bez početne brzine, bez trenja, kako bi u najkraće vrijeme prevalilo put iz više točke u nižu.
Joseph Louis de Lagrange je jedan od primijenjenih operatora nazvao varijacija, a Leonhard Euler je u radu Elementi računa varijacija (1766) dao ime računu varijacija. Za razvoj računa varijacija važni su radovi Jeana Baptiste le Ronda d’Alemberta, Carla Gustava Jacobija, Karla Weierstrassa, Davida Hilberta i dr.
Primjena
Klasični problem računa varijacija određivanje je geodetskih linija na nekoj plohi, odn. najkraćih spojnica dviju zadanih točaka na toj plohi (npr. u ravnini su geodetske linije dijelovi pravaca, a na sferi su to lukovi glavnih kružnica).
Mnogi zakoni fizike, a i osnovni fizikalni principi, iskazuju se u varijacijskom obliku. Tako se npr. u okviru klasične fizike svjetlost iz jedne točke u drugu širi onom putanjom koju prevaljuje u najkraćem vremenu (→ princip najmanjega djelovanja).
Račun varijacija primjenjuje se u mehanici, optici, kvantnoj mehanici i općoj teoriji relativnosti, teoriji optimizacije, za modeliranje i rješavanje matematičkih, fizikalnih i inženjerskih problema, od prigušivanja neželjenih vibracija u mehaničkim i građevinskim konstrukcijama i oblikovanja zrakoplovnih krila do programiranja mekog slijetanja svemirskih letjelica.