teorija vjerojatnosti, grana matematike koja proučava odnose među slučajnim događajima. Objekti su teorije vjerojatnosti slučajne varijable i stohastički procesi.
Prostor vjerojatnosti je skup elementarnih događaja {E1, E2, …, En}, a svakom je elementarnom događaju pridružena vjerojatnost, broj p (Ek), veći ili jednak nuli i manji ili jednak jedinici, 0 ≤ p (Ek) ≤ 1, vjerojatnost elementarnoga događaja Ek, i to tako da je zbroj vjerojatnosti elementarnih događaja cijelog skupa jednak jedinici p (E1) + p (E2) + … + p (En) = 1.
Slučajni događaj je postupak koji se uz definirane uvjete može ponavljati a ima najmanje dva moguća ishoda.
Složeni događaj ili jednostavno događaj je bilo koji podskup prostora elementarnih događaja.
Vjerojatnost složenog događaja definira se kao zbroj vjerojatnosti elementarnih događaja od kojih je složeni događaj sastavljen. Npr. kod bacanja igraće kocke elementarni događaji Ek, 1 ≤ k ≤ 6, jesu jednako mogući (pretpostavka o idealnoj kocki) i svaki elementarni događaj ima vjerojatnost 1/6. Vjerojatnost složenog događaja npr. da »padne 1 ili 2 ili 3« jednaka je tada 1/6 + 1/6 + 1/6 = 1/2. Općenito: ako su svi elementarni događaji Ek, 1 ≤ k ≤ n nekoga prostora vjerojatnosti jednako mogući, vjerojatnost svakog od njih jednaka je 1/n. Vjerojatnost složenoga događaja sastavljenog od m elementarnih događaja jednaka je m/n (vjerojatnost je jednaka količniku broja povoljnih i broja svih mogućih događaja).
Slučajna varijabla je svaka realna funkcija definirana na prostoru vjerojatnosti. Ako je X slučajna varijabla, a x1, …, xn njezine vrijednosti, te ako se svakomu xk pridruži vjerojatnost f (xk) događaja A, definiranoga zahtjevom X (A) = xk, onda to pridruživanje definira razdiobu vjerojatnosti slučajne varijable X. Ako je X slučajna varijabla, a f njezina razdioba vjerojatnosti, onda se broj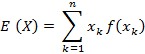 
naziva matematičko očekivanje slučajne varijable X.
Zakon velikih brojeva služi za određivanje vjerojatnosti s pomoću velikoga broja pokusa ili promatranja (statistička vjerojatnost).
Teoriju vjerojatnosti započeli su razvijati u XVII. st. kao teoriju hazardnih igara Blaise Pascal, Pierre de Fermat i Christian Huygens a matematičkom disciplinom postala je radovima Jakoba Bernoullija, Pierrea Simona de Laplacea, Carla Friedricha Gaussa, Pafnutija Ljvoviča Čebišova i dr. Na suvremenoj aksiomatskoj osnovi teoriju vjerojatnosti razvili su Andrej Andrejevič Markov, Andrej Nikolajevič Kolmogorov, Harald Cramér i dr.
