Gaussov algoritam (Gaussova eliminacija) [gạus~], najstariji, najjednostavniji i najpoznatiji niz matematičkih operacija, koji je predložio Carl Friedrich Gauss, s pomoću kojega se rješava sustav linearnih jednadžbi eliminiranjem pojedinih nepoznanica.
Prvo se u jednoj od jednadžbi jedna od varijabli izrazi s pomoću ostalih varijabli (eliminira), a zatim se dobiveni izraz uvrsti u ostale jednadžbe. Tako se broj jednadžbi i broj varijabli smanji za jedan. Zamjena varijabli ponavlja se i proces smanjivanja broja jednadžbi i varijabli se nastavlja dok ne ostanu samo jedna jednadžba i jedna varijabla. Kad se ta jednadžba riješi, postupak se odvija u suprotnom smjeru i jedna po jedna izračunavaju se sve varijable.
Za prilagođavanje rješavanja sustava linearnih jednadžbi računalu koristi se prikaz sustava jednadžbi s pomoću matrice sustava. Matrica sustava je tablični zapis koeficijenata jednadžbi sustava i slobodnih članova u kojem redci odgovaraju pojedinim jednadžbama, a stupci pojedinim nepoznanicama. Na primjer, sustavu jednadžbi
x + y + z = 4
x – y + z = 2
2x + y – z = 1
odgovara matrični prikaz
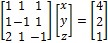 .
.
Cilj je Gaussova algoritma matricu sustava svesti na oblik iz kojeg je lako očitati rješenje sustava, tj. na dijagonali matrice sustava dobiti jedinice, a ispod dijagonale i iznad nje nule. Pri prilagođavanju matrice sustava primjenjuju se elementarne transformacije koje mijenjaju matricu, ali ne i skup rješenja: zamjena dvaju redaka, množenje nekog retka brojem koji nije nula, pribrajanje jednog retka drugomu. Rješenju sustava jednadžbi iz navedenog primjera x = 1, y = 1, z = 2 odgovara matrični zapis
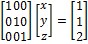 .
.