trigonometrijska funkcija, periodična funkcija kutne varijable određene položajem točke na brojevnoj kružnici: sinus (znak sin), kosinus (cos), tangens (tan), kotangens (cot), uz rjeđe upotrebljavane sekans (sec) i kosekans (csc). Elementarno se definira za vrijednosti argumenta x iz intervala (0, 90°), odnosno (0, π/2), shvaćenoga kao šiljasti kut pravokutnoga trokuta nasuprot kateti duljine a, dakle: sin x = a/c, cos x = b/c, tan x = sin x/cos x = a/b, cot x = 1/tan x = b/a, csc x = 1/sin x = c/a, sec x = 1/cos x = c/b.
Vrijednost trigonometrijske funkcije ovisi samo o kutu, a ne o duljinama stranica trokuta (zbog sličnosti trokuta a : b : c = a': b' : c').
Opća definicija trigonometrijske funkcije za sve vrijednosti argumenta x iz intervala 0 ≤ x ≤ 2π temelji se na brojevnoj kružnici. Ako je T bilo koja točka brojevne kružnice, a x mjera kuta ∡ AOT u radijanima, koja je jednaka duljini luka AT, tada je sin x ordinata, a cos x apscisa točke T, tj. T (cos x, sin x). Nadalje je tan x ordinata točke B, a cot x apscisa točke C, dok su sec x, odnosno csc x duljine dužina OC odnosno OB uzetih s predznakom koji imaju pripadni sinus, odn. kosinus. Na proizvoljne argumente te se definicije proširuju zahtjevima: sin (x + 2 kπ) = sin x, cos (x + 2 kπ) = cos x, tan (x + kπ) = tan x i cot (x + kπ) = cot x za sve k = ± 1, ± 2 … Odatle se vidi da su trigonometrijske funkcije periodične funkcije, i to sinus i kosinus s periodom 2π, a tangens i kotangens s periodom π.
Grafički prikaz trigonometrijske funkcije sinus u pravokutnom Kartezijevu koordinatnom sustavu je sinusoida, funkcije kosinus kosinusoida, funkcije tangens tangensoida itd.
Trigonometrijski identiteti povezuju trigonometrijske funkcije.
Eulerova relacija cos x + i sin x = eix , gdje je i imaginarna jedinica a e Eulerov broj, povezuje funkcije sinus i kosinus i kompleksnu eksponencijalnu funkciju.
Vrijednosti trigonometrijskih funkcija za neke posebne brojeve
| x |
0 |
π/6 |
π/4 |
π/3 |
π/2 |
2π/3 |
3π/4 |
5π/6 |
π |
| sin x |
0 |
1/2 |
√ 2 /2 |
√ 3 /2 |
1 |
√ 3 /2 |
√ 2 /2 |
1/2 |
0 |
| cos x |
1 |
√ 3 /2 |
√ 2 /2 |
1/2 |
0 |
–1/2 |
–√ 2 /2 |
–√ 3 /2 |
–1 |
| tan x |
0 |
√ 3 /3 |
1 |
√ 3 |
±∞ |
–√ 3 |
–1 |
–√ 3 /3 |
0 |
| cot x |
±∞ |
√ 3 |
1 |
√ 3 /3 |
0 |
–√ 3 /3 |
–1 |
–√ 3 |
±∞ |
Redovi trigonometrijskih funkcija
Trigonometrijske funkcije mogu se razviti u beskonačne redove potencija, npr.:
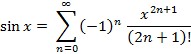 ,
,
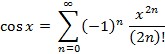 ,
,
koji konvergiraju za sve realne (a i kompleksne) brojeve x.
Derivacije i integrali trigonometrijskih funkcija
| funkcija |
derivacija funkcije |
integral funkcije (C je konstanta integracije) |
| f(x) |
f '(x) |
∫ f(x)dx |
| sin x |
cos x |
–cos x + C |
| cos x |
–sin x |
sin x + C |
| tan x |
sec² x = 1 + tan²x |
–ln |cos x| + C |
| cot x |
csc² x = –(1 + cot²x) |
ln |sin x| + C |
| sec x |
sec x tan x |
ln |sec x + tan x| + C |
| csc x |
–csc x cot x |
–ln |csc x + cot x| + C |
Inverzne funkcije trigonometrijskih funkcija
Arkus funkcija je inverzna funkcija trigonometrijske funkcije: za sinus je to funkcija arkus sinus (znak arcsin), za kosinus je arkus kosinus (arccos), za tangens arkus tangens (arctan), za kotangens arkus kotangens (arccot) itd.
Mjerenje kutova
Goniometrija je dio trigonometrije koji se bavi mjerenjem kutova i trigonometrijskim vezama među njima.