Laplace [lapla's], Pierre Simon de, francuski astronom i matematičar (Beaumont-en-Auge, Calvados, 28. III. 1749 – Pariz, 5. III. 1827). Studirao na Sveučilištu u Caenu, potom se u Parizu usavršavao kod Jeana Baptistea le Rond d’ Alemberta, temeljem čije je preporuke predavao matematiku u École royale militaire (1771–76). Bio je državni ispitivač iz matematike za topničke kadete, od 1795. radio u Uredu za geografske koordinate kojega je više puta bio predstojnik. Otkrio je zakon o nepromjenljivosti srednjih vremena gibanja planeta oko Sunca (1773) i ovisnost sekularnih promjena (malih odstupanja do kojih dolazi u dugom razdoblju; lat. saeculum: stoljeće) u ekscentricitetu Zemljine putanje o gravitaciji Mjeseca. Izračunao je putanje prvih triju Jupiterovih satelita te proučavao plimu i oseku (Laplaceove plimne jednadžbe, 1776). Pri pronalaženju metoda za određivanje putanje kometa došao je u akademski spor s Ruđerom Josipom Boškovićem (1776). Rane je radove iz astronomije usustavio u djelu Teorija pokreta i eliptične putanje planeta (Théorie du mouvement et de la figure elliptique des planètes, 1784), a hipotezu o nastanku Sunčeva sustava iz maglice (oblaka tvari), danas poznatu kao Kant-Laplaceova hipoteza, objavio je 1796. u djelu Sustav svijeta (Exposition du système du monde, I–II) te dalje izlagao u Raspravi o nebeskoj mehanici (Traité de mécanique celeste, I–V, 1799–1825) u kojoj razrađuje postavke iz djela Isaaca Newtona Matematički principi filozofije prirode. Bavio se i drugim područjima matematičke fizike, npr. teorijom elektriciteta, kapilarnosti tekućina i specifičnim toplinskim kapacitetima čvrstih tijela. U tumačenje znanstvenih podataka uveo je teoriju vjerojatnosti, pridonijevši njezinu razvoju kao matematičke discipline te je u djelu Analitička teorija vjerojatnosti (Théorie analytique des probabilités, 1812) dao klasičnu definiciju vjerojatnosti, a ta je teorija polazište i njegova Filozofskog eseja o vjerojatnostima (Essai philosophique sur les probabilités, 1814) u kojem je zastupao ideje sveopćega determinizma (tzv. Laplaceov demon kao shvaćanje po kojem je s pomoću zakona klasične mehanike moguće izračunati svako prošlo ili buduće stanje ako netko, npr. demon, zna sve položaje i količine gibanja svih atoma u svemiru). Kao jedan od najistaknutijih francuskih znanstvenika svojega doba, od 1773. je bio član francuske Akademije znanosti, od 1816. Francuske akademije, od 1822. Američke akademije umjetnosti i znanosti, 1799–1814. senator, 1806. dobio je naslov grofa, a 1817. markiza. Po njem je nazvan planetoid (4628 Laplace).
Laplaceova transformacija pretvara funkciju realne varijable u funkciju kompleksne varijable, a diferencijalne jednadžbe u algebarske jednadžbe koje je lakše riješiti.
Laplaceov razvoj je postupak za snižavanje reda determinante.
Laplaceov operator je linearni diferencijalni operator, Δ = ∂²/∂x² + ∂²/∂y² + ∂²/∂z² , kojim se može djelovati na neku funkciju. Pojednostavnjuje matematički zapis.
Laplaceova diferencijalna jednadžba za neku funkciju φ (x, y, z) glasi: Δφ = ∂²φ/∂x² + ∂²φ/∂y² + ∂²φ/∂z² = 0. Funkcije koje zadovoljavaju tu jednadžbu nazivaju se Laplaceove, harmonijske ili potencijalne funkcije. U elektrostatici, Poissonova jednadžba postaje Laplaceova onda kada gustoća naboja ρ (x, y, z) iščezava, pa se dobije ΔU(x, y, z) = 0.
Laplaceova jednadžba pokazuje u akustici ovisnost brzine zvuka o svojstvima plina u kojem se zvuk širi. Izvedena je iz Newtonove jednadžbe za brzinu zvuka u elastičnim sredstvima v = √ E / ρ , gdje je v brzina zvuka, E modul elastičnosti, a ρ gustoća sredstva. Laplace je dokazao da se u jednadžbi za plin modul elastičnosti može zamijeniti umnoškom tlaka (p) i omjera specifičnih toplinskih kapaciteta pri konstantnom tlaku (cp) i konstantnom volumenu (cv) zato što se zgušnjavanje i razrjeđivanje slojeva plina u zvučnom titranju odvija adijabatski. Dakle, brzina zvuka u plinu iznosi v = √ (γp) / ρ , gdje je γ = cp/cv. Pri normalnom tlaku zraka, Laplaceova formula za brzinu zvuka daje vrijednost 330 m/s, što odgovara eksperimentalno utvrđenoj vrijednosti.
Laplaceov zakon daje jakost magnetskoga polja koje djeluje u točkama prostora, a uzrokuje ga električna struja koja teče kroz vodič: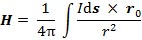 
, gdje je I jakost električne struje, s duljina vodiča, r udaljenost između vodiča i točke u kojoj se opaža jakost magnetskoga polja H, a r0 jedinični vektor u tom smjeru. Ukupno magnetsko polje u promatranoj točki rezultat je doprinosa električne struje kroz cijeli promatrani vodič u danoj strujnoj petlji.
