integralni račun, dio infinitezimalnog računa u kojem se proučavaju metode izračunavanja vrijednosti integrala.
Povijesni razvoj
Početci integralnoga računa mnogo su stariji od nastanka diferencijalnoga računa. Već je metoda kojom je Arhimed izračunavao ploštinu kruga i segmenta parabole zametak je integralnoga računa. Tu metodu, proširivši je i na druge probleme, nastavili su i razvijali u XVII. st. Johannes Kepler, Francesco Bonaventura Cavalieri, Galileo Galilei, Blaise Pascal i Pierre de Fermat, sve dok Gottfried Wilhelm Leibniz i Isaac Newton nisu postavili temelje na kojima su Augustin-Louis Cauchy, Karl Weierstrass i dr. u XIX. st. od integralnog računa stvorili jedno od najznačajnijih sredstava matematičke analize. U novije se doba iz integralnoga računa razvila teorija mjere, koja je naišla na svestranu primjenu, posebno u teoriji vjerojatnosti i teoriji diferencijalnih jednadžbi.
Vrste integrala
Određeni integral funkcije f definira se kao ploština područja ispod grafa funkcije f i iznad osi x ako je f realna funkcija definirana na segmentu [a, b] realnih brojeva (a ≤ x ≤ b), te ako poprima samo pozitivne vrijednosti. Ako funkcija f poprima i negativne vrijednosti, ploštinu područja iznad grafa funkcije a ispod osi x uzima se s negativnim predznakom. Određeni integral funkcije f na segmentu [a, b] je broj a označuje se sa:
Neodređeni integral od funkcije f je funkcija F kojoj je derivacija jednaka f, tj. F′(x) = f (x); F se naziva i primitivna funkcija funkcije f. Budući da je derivacija konstante jednaka nuli, F + C također je primitivna funkcija od f za bilo koju konstantu C. Dodavanjem konstanata jednoj primitivnoj funkciji dobivaju se sve primitivne funkcije od f. Neodređenim integralom često se naziva i skup svih primitivnih funkcija od f; taj se skup označuje sa:
Osnovni teorem integralnog računa govori o vezi između određenog i neodređenog integrala i glasi: ako je F primitivna funkcija od f, tada je određeni integral funkcije f na segmentu [a, b] jednak razlici vrijednosti funkcije F na krajevima toga segmenta:
b
⌠
⌡
a |
ƒ(x) dx = F(b) − F(a). |
S pomoću tog teorema mogu se efektivno izračunati određeni integrali mnogih elementarnih funkcija. Također slijedi da se primitivna funkcija može izračunati s pomoću određenog integrala:
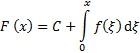 ,
,
(gdje je C bilo koja konstanta).
Primjena integralnoga računa
Primjenom integralnoga računa mogu se riješiti mnogi problemi matematike, mehanike i tehnike. Tako se npr. volumen V tijela koje nastaje rotacijom luka krivulje y = f (x) oko osi x može izračunati s pomoću određenog integrala po formuli: 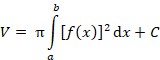 .
.
Integralni račun služi i za izračunavanje duljine luka krivulja, a s pomoću dvostrukih i višestrukih integrala mogu se izračunati oplošja i volumeni različitih tijela.