zakrivljenost, u matematici, zakrivljenost krivulje odnosno plohe, mjera njihova odstupanja od pravocrtnosti odnosno ravnosti. U diferencijalnoj geometriji uvode se dvije vrste zakrivljenosti krivulje: fleksija i torzija.
Fleksija (znak k) krivulje u nekoj njezinoj točki definira se kao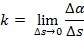 
, gdje je Δα kut koji zatvaraju tangente krivulje u njezinim dovoljno bliskim točkama, a Δs duljina luka između dirališta tih tangenata. Polumjer zakrivljenosti krivulje u nekoj točki je polumjer ρ oskulacijske kružnice koja dodiruje krivulju u toj točki i jednak je ρ = 1/k. Središte zakrivljenosti krivulje u nekoj točki je središte oskulacijske kružnice koja dodiruje krivulju u toj točki. Za krivulju zadanu s r = r (s) vrijedi 
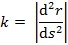. Zakrivljenost krivulje u nekoj točki s pomoću oskulacijske kružnice u toj točki prvi je 1686. definirao Gottfried Wilhelm Leibniz. Infleksija je promjena zakrivljenosti iz pozitivne u negativnu.
Torzija (znak τ) krivulje u nekoj njezinoj točki definira se kao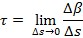 
, gdje je Δβ kut što ga zatvaraju oskulacijske ravnine u bliskim točkama krivulje, odnosno njihove normale (tzv. binormale). Za krivulju r = r (s) vrijedi: 
.
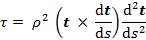Zakrivljenost plohe u nekoj njezinoj točki T svodi se na zakrivljenosti njezinih normalnih presjeka u toj točki, tj. presjeka te plohe u točki T. Među normalnim presjecima u točki T postoje dva s ekstremnim zakrivljenostima, maksimalnom k1 i minimalnom k2, a ravnine tih presjeka međusobno su okomite. S pomoću njih definirane su srednja zakrivljenost H = 1/2 (k1 + k2) i Gaussova zakrivljenost K = k1k2.
Ako je zbroj kutova unutar trokuta koji leži na nekoj zakrivljenoj plohi veći od 180°, Gaussova zakrivljenost je pozitivna, a ako je manji od 180°, Gaussova zakrivljenost je negativna. Npr. Gaussova zakrivljenost hiperboloida je negativna (K < 0), ravnine jednaka nuli (K = 0), sfere pozitivna (K > 0), a kod torusa ovisi o dijelu na kojem se promatra. Carl Friedrich Gauss (1827) dokazao je da je Gaussova zakrivljenost invarijantna pri svim izometričkim transformacijama plohe (tzv. theorema egregium). Na tom se temelji cjelokupna unutarnja geometrija neke plohe.
